Abstract
Mathematics become important and frequently applies in human daily life, especially involve with numbering and operational. The historical of mathematical development in numbering are exist in Egyptian, Greek, Roman, Chinese, Mayan and Hindu-Arabic; and operational involve in Egyptian, Babylon, Hindu, Chinese, and Arabia. The numbers and operational is continuously developed until today. Various researchers is still work hard to improve the numbers and operational through variety of modeling and statistical analysis. Therefore, the invaluable advances will improve the quality of human life through the mathematical subject.
Keywords: mathematics, history, numbering, operational, quality life.
Citation of Article:
Ping, O.W., & Hua, A.K. (2018). History of Mathematical Number and Operational: A Review. International Journal for Social Studies, 4(6), 82-94.
INTRODUCTION
Mathematics is knowledge about researching in quantity, structure, space and so on [5-7]. Among the mathematics that important and frequently involve in human daily life is the numbering and the operational. During ancient time, humans have been applying calculation in their lives [1-4; 8-9]. As an evidenced, the discovery of the tally marks in Zaire in 6000 B.C. (Figure 1) and the knot on a rope in Peru (Figure 2).
DISCUSSIONS
The History of Numbering
In 3000 B.C. to 2000 B.C., the numbering systems are known as cuneiform, which exist in Babylonian times. This numbering system only uses 2 symbols to represent the numbers, namely one and ten. The placing numbering is unique and it has own structure to represent each number. Babylonian numbering system only has the number one to number fifty nine (Figure 5). The number sixty and above, will requires the calculation by using the power based of sixty and the symbols have to be multiplied by 60 to get the real value (Figure 6). One of the disadvantages of the numbering system of Babylonian is the confusing of value placing. Therefore, earlier Babylonian mathematicians have created overlapping triangular shape to differentiate the value of places. Additional, the Babylonian numbering does not recognize the multiplication tables as a number in their numbering system.
In Greek numbering system, it developed around 600 B.C. up to 450 B.C., and has 2 type of principles namely acrophonic and alphabet. Acrophonic principle system using the first letter of the name of the number, for example 5 is call penta, and the symbols is
Roman numbering system is developed in 500 A.D. and the system is still use until today. The basis symbol is Roman numbering of I (1), V (5), and X (10) (Figure 9). The system is also involve with operational of add and minus whereby if a smaller number is on the left side then added will be involve. For the minus operational, a larger number will be on the left side and a smaller number will be on right side. Therefore, it will involve a lot of symbols when larger numbers is involved. Then it came with the L, C, D, and M, representing a value of 50, 100, 500, and 1000 (Figure 10). This symbol appears from the changes of V and X.
Chinese numbering system is start around 213 B.C. in China. It uses 18 rod and 14 Chinese writing. Up-to-date, only the 14 Chinese writing is still used to represent the number (Figure 11), yet the 18 rod have disappeared (Figure 12).
At 300 B.C., Mayan numbering system already exist and this numbering system using two basic symbols namely point represent as 1 and horizontal line represent as 5 (Figure 13). On that time, multiplication table symbols are introduced. Mayan numbering system is more advanced than the Babylonian numbering system. Mayan numbering system is also involved in the adding operation and use to the power of based 20. The method of calculation is very unique as it is written vertically as in Figure 14.
Lastly, the Hindu-Arabic numbering system is widely used in nowadays. Hindu-Arabic numbering system developed at around 600 A.D. and uses 10 symbols of 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. This system is unique because it has own placing and uses the bases of 10. Hindu-Arabic numbering system of the earliest countries starting to apply is from India, and its start to expand into other countries. When it expanded to other countries, the system applied the changes for flexibility with the culture of that country until the updated of Hindu-Arabic numbering system was introduced (Figure 15).
Since 2000 B.C., there are four types of basic operational being recorded until these days in Egypt and Babylon, namely added, subtract, multiple and divide. The tools for calculation of plus and minus are abacus or counting board. Figure 16 showing the founder, Pythagoras using abacus for conducting the operational and Boethius uses pen and paper. Meanwhile, Figure 17 explains the calculation of addition operation of the two numbers is performed using counting board. The counting board is divided according to the place, which is one (I), ten (X), hundred (C), thousands (M) and so on. If the ‘room’ has reached to a maximum of 10 seeds, then the number will be removed and the seeds are added to another site which is subsequently higher than the room. So, the minus operation are the same as additional operation, which can be shown in Figure 18.
Multiple and divide methods of Egypt is recorded in The Rhind Papyrus, is carry out using duplication or two consecutive double. The Rhind Papyrus is important document for the Egyptian mathematician. The document length is 5m, and there are 84 issues provided by a writer named Ahmed in 1600 B.C. based on the sources. For example, multiple of 69 with 19, the first duplication of 69 are 1 and 69, next duplication is between 2 and 138, 4 with 276, 8 with 552, and 16 with 1104. 19 is the sum of 16, 2 and 1, which shows that result of multiple 69 with 19 is the additional operation between 1104, 138 and 69, is 1311. The divide operation are also have same process.
Mathematicians Hindu fascinated with numbers, whether involving ordinary arithmetic operations or solution for defined or undefined equations. Addition and multiplication method used by Hindu is the same as the modern methods that we use today. Hindu multiplication is commonly used lattice multiplication, can also be known as gelosia multiplication, multiplication cell or multiplication grille quadrilateral. The existing of gelosia multiplication is unclear, but it was widely used in 12th century, and was brought from India to China and Arabia. There are two ways for this lattice multiplication. For example, 537 multiplied by 24. The number of 537 is written on the lattice, while the number of 24 can be written on the left side of the lattice under or to the right from the top. The product of partial occupies a square cell. Digits in diagonal rows are added and the product is read from bottom to top or from right to left on the bottom. Figure 19 shows two ways Hindu lattice multiplication.
The pattern of long division is known as "scratch method" or "method galley ", which also comes from India. Figure 20 show ‘Ghali’ division of the 16th century, which from a manuscript monk Venetian that is unpublished. The title of the work is "Opus Arithmetica D. Honorati Veneti monachj coenobij S. Lauretig". Method galley is almost the same as the divide method in modern era, but there is little difference. In the galley, the numbers can be written in the middle, where the calculation involves with the cutting digit and the less number will be placed on top. Hence, the balance will exist above and divide results is located on the right hand side. The number position in column position is important than the number in line. For example, 2957 is not written in the same line, but must be written from left to right.
These methods can be explain more detail by using 44977 divide with 382, which can be shown as below for divide operational of modern era with ghali method.
Chinese multiplication is performed using arithmetic counting board. For example, 83 X 27 = 2241. The calculation is started with the 8 times 2 and the product of 16 written on the digit 2 in the same column. Then, the calculation of 8 times 7 is 56 and is also written on the digit 7 in the same column. Both the product gets added 27 216. Then, there are 27 will be moved one space to the right and one row is added. The process was repeated, and the result of 3 times 2 times 6 written on 2 digits in the same column, 3 times 7 is 21 and is also written on the digit 7 in the same column. Finally, added the entire number and the division result provided as 2241. Similarly, China carried out using arithmetic counting board.
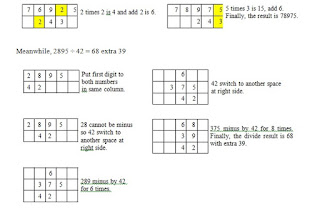
The same concept will be used in the Chinese’s divide operational, only the process of added of the multiplication is changed to minus. This is because 18 are not able to be minus by 71, then 71 is moved from one space to the right hand side. The minus process for 71 is repeated until the number in the row-middle cannot be conducted. Again, 71 moved one space to the right and the minus process of 71 is repeated. Both minus and switch process for 71 is repeatedly executed until the last digit. Finally, the result will be 265.
Multiple by Ibn Labban for 325 X 243 = 2241 can be describe as below:
References
[9] Samian, A. L. (1992). Sejarah matematik. Kuala Lumpur: Dewan Bahasa dan Pustaka.
Lastly, the Hindu-Arabic numbering system is widely used in nowadays. Hindu-Arabic numbering system developed at around 600 A.D. and uses 10 symbols of 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. This system is unique because it has own placing and uses the bases of 10. Hindu-Arabic numbering system of the earliest countries starting to apply is from India, and its start to expand into other countries. When it expanded to other countries, the system applied the changes for flexibility with the culture of that country until the updated of Hindu-Arabic numbering system was introduced (Figure 15).
The History of Operational
The Egypt and The Babylon
Multiple and divide methods of Egypt is recorded in The Rhind Papyrus, is carry out using duplication or two consecutive double. The Rhind Papyrus is important document for the Egyptian mathematician. The document length is 5m, and there are 84 issues provided by a writer named Ahmed in 1600 B.C. based on the sources. For example, multiple of 69 with 19, the first duplication of 69 are 1 and 69, next duplication is between 2 and 138, 4 with 276, 8 with 552, and 16 with 1104. 19 is the sum of 16, 2 and 1, which shows that result of multiple 69 with 19 is the additional operation between 1104, 138 and 69, is 1311. The divide operation are also have same process.
The Hindu (multiple and divide operational)
These methods can be explain more detail by using 44977 divide with 382, which can be shown as below for divide operational of modern era with ghali method.
Chinese Multiple and Divide Operational
The same concept will be used in the Chinese’s divide operational, only the process of added of the multiplication is changed to minus. This is because 18 are not able to be minus by 71, then 71 is moved from one space to the right hand side. The minus process for 71 is repeated until the number in the row-middle cannot be conducted. Again, 71 moved one space to the right and the minus process of 71 is repeated. Both minus and switch process for 71 is repeatedly executed until the last digit. Finally, the result will be 265.
Arabia Multiple and Divide Operational
Conclusion
According to the history of mathematics, the numbers and operational is continuously developed until today. Yet, various researchers is still work hard to improve the numbers and operational through variety of modeling and statistical analysis. Therefore, the invaluable advances will improve the quality of human life through the mathematical subject.
[1] Boyer, C. B., Merzbach, U. C., & Manan, A. A. (2007). Sejarah matematik :a history of mathematics. Kuala Lumpur: Institut Terjemahan Negara Malaysia.
[2] Bruno, L.C. (1999). Mathematicians: The history of Math Discoveries Around the World. United States of America: Farmington Hills.
[3] Burton, D.M. (2007). The History of Mathematics: An introduction(6th ed.). Singapore: McGraw Hill.
[4] Gary, L. M., William, F. B. & Blake, E. P. (2009). Mathematics For Elementary Teacher: A Contemporary Teachers(7th ed.).Singapore: John Wiley & Sons.
[5] Hua, A. K. (2016). Pengenalan Rangkakerja Metodologi dalam Kajian Penyelidikan: Satu Kajian Literatur. Malaysian Journal of Social Sciences and Humanities, 1(2), 17-24.
[6] Hua, A. K. (2016). Introduction to Metodology Framework in Research Study. Malaysian Journal of Social Sciences and Humanities (MJSSH), 1(2), 17-24.
[7] Hua, A. K. (2016). Introduction to Framework Metodology in Research Study. Malaysian Journal of Social Sciences and Humanities (MJSSH), 1(4), 42-52.
[8] Mastin, L. (2010). The Story of Mathematics. Retrieved from